Чотирикутники

Означення

Чотирикутник — це фігура, що складається з чотирьох вершин та чотирьох відрізків, які їх послідовно сполучають. Жодні три вершини не лежать на одній прямій. Сума всіх внутрішніх кутів будь-якого опуклого чотирикутника завжди дорівнює $36 0^{\circ}$ .

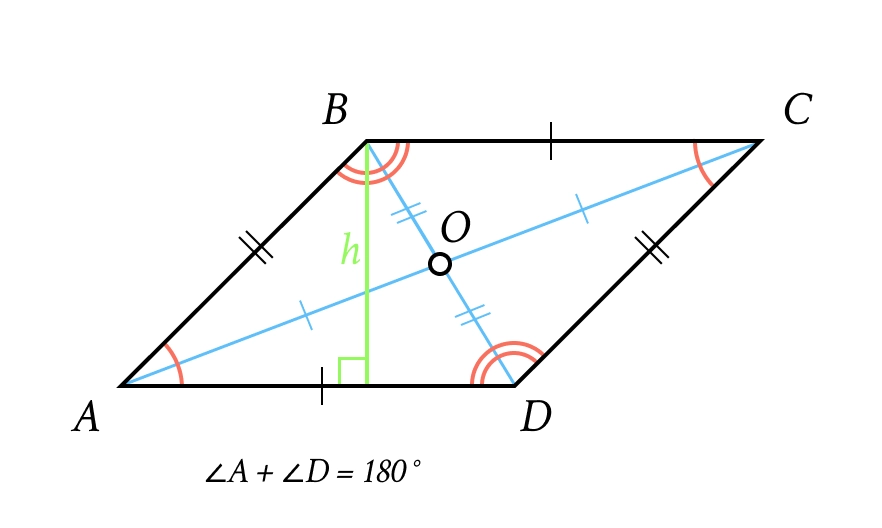
1. Паралелограм

Це «фундаментальна» постать. Якщо ви знаєте властивості паралелограма, ви автоматично знаєте половину властивостей прямокутника, ромба та квадрата.

Властивості сторін та кутів: Протилежні сторони паралельні та рівні. Протилежні кути рівні. Сума кутів, прилеглих до однієї сторони, дорівнює 180°.
Діагоналі: Перетинаються і точкою перетину діляться навпіл.
Основні формули площі:
$S = a \cdot h_{a}$ (сторона на висоту);
$S = a \cdot b \cdot sin α$ (через дві сторони та кут між ними);
$S = \frac{1}{2} d_{1} d_{2} sin ϕ$ (через діагоналі та кут між ними).

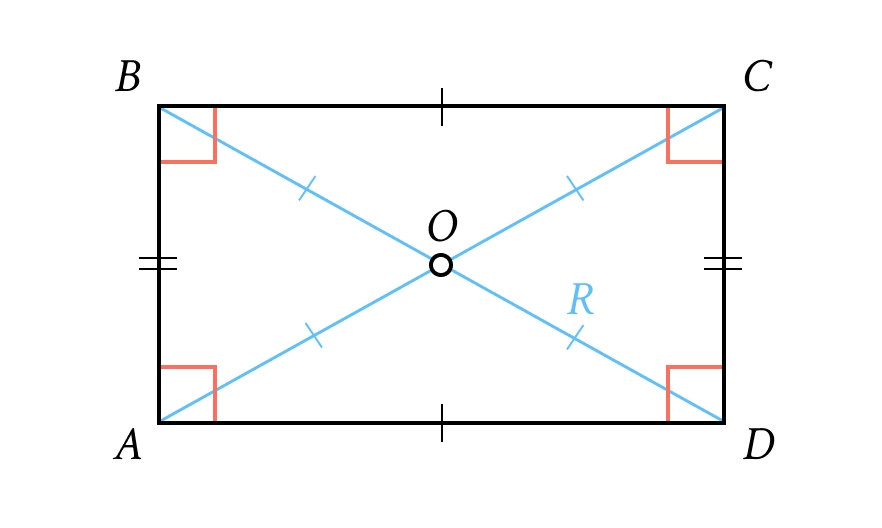
2. Прямокутник

Це паралелограм, у якого всі кути по 90°.

Особлива властивість: Діагоналі прямокутника рівні ( $d_{1} = d_{2}$ ).
Центр кола: Навколо будь-якого прямокутника можна описати коло. Його центр лежить у точці перетину діагоналей, а радіус $R = \frac{d}{2}$ .
Площа: $S = a \cdot b$ .

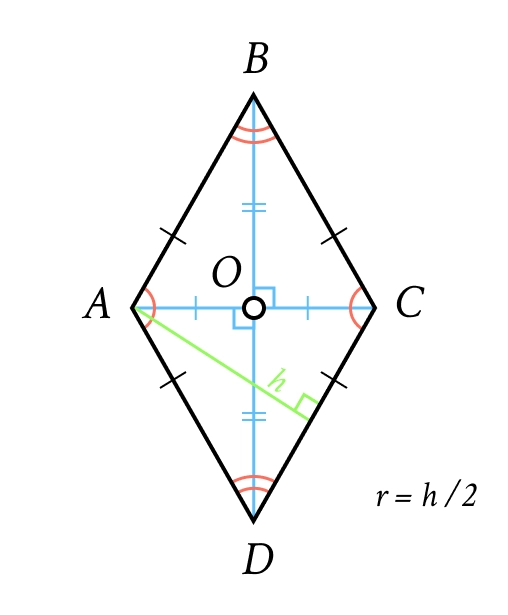
3. Ромб

Це паралелограм, у якого всі сторони рівні.

Властивості діагоналей: Вони перпендикулярні ( $d_{1} ⊥ d_{2}$ ) і є бісектрисами кутів ромба.
Радіус вписаного кола: У ромб завжди можна вписати коло. Його радіус $r = \frac{h}{2}$ .
Площа: $S = \frac{1}{2} d_{1} d_{2}$ (найпопулярніша формула для ромба).

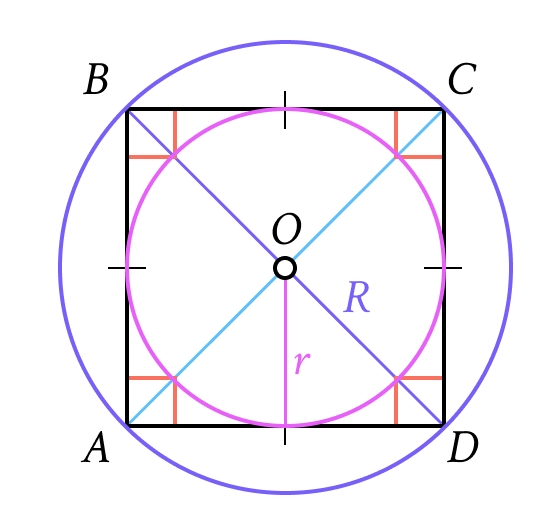
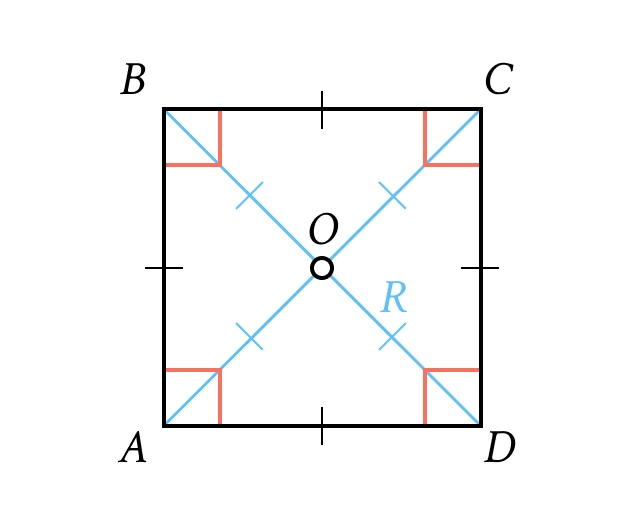
4. Квадрат

Король фігур. Має всі властивості прямокутника та ромба одночасно.

Діагональ квадрата: $d = a 2$ .
Площа: $S = a^{2}$ або $S = \frac{d ^{2}}{2}$ .

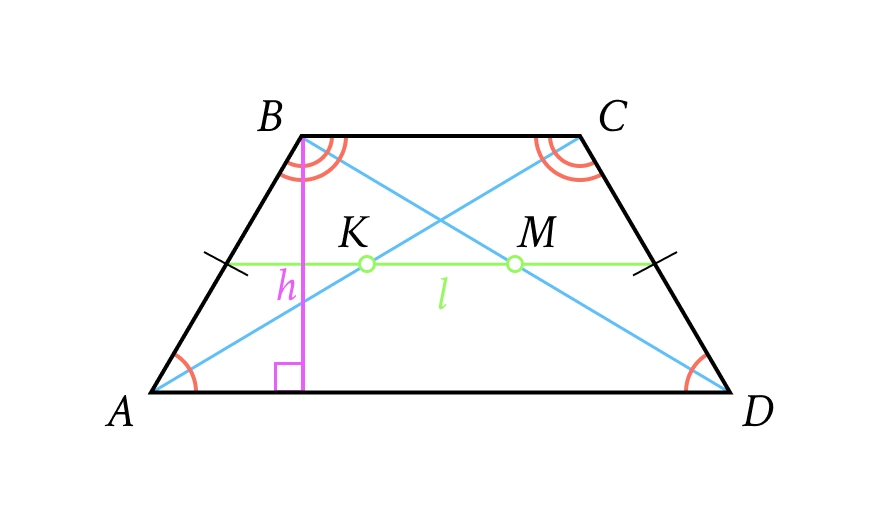
5. Трапеція

Чотирикутник з однією парою паралельних сторін (основи $a$ та $b$ ).

Середня лінія ( $l$ ): $l = \frac{a + b}{2}$ . Паралельна основам.
Рівнобічна трапеція: Має рівні бічні сторони, рівні кути при основах та рівні діагоналі. Навколо неї завжди можна описати коло.
Площа: $S = \frac{a + b}{2} \cdot h = l \cdot h$ .

6. Вписані та описані чотирикутники (Критерії)

Вписаний: Суми протилежних кутів рівні 180°. ( $∠ A + ∠ C = ∠ B + ∠ D = 18 0^{\circ}$ ).
Описаний: Суми протилежних сторін рівні. ( $a + c = b + d$ ).