Теорія ймовірностей

Означення

Теорія ймовірностей вивчає закономірності випадкових явищ. Результати експериментів називають наслідками, а будь-яке твердження про них — подією.

Класичне означення ймовірності

Ймовірністю події $A$ називають відношення кількості сприятливих результатів до загальної кількості всіх рівноможливих наслідків.

Приклад: у колоді 36 карт. Ймовірність витягнути карту чирвової масті (яких 9) становить $P(A)=\frac{9}{36}=0,25$.

Класифікація подій

Протилежні події: подія $\bar{A}$ відбувається тоді, коли не відбувається $A$. Сума їхніх ймовірностей завжди дорівнює 1: $P(\bar{A})=1-P(A)$.

Основні теореми

• Теорема додавання (для несумісних подій): ймовірність появи або $A$, або $B$ дорівнює сумі їхніх ймовірностей: $P(A+B)=P(A)+P(B)$.

• Теорема множення (для незалежних подій): ймовірність спільної появи двох подій дорівнює добутку їхніх ймовірностей: $P(A\cdot B)=P(A)\cdot P(B)$.

• Геометрична ймовірність: відношення мір (площ, довжин) частин фігури. $P=\frac{S(A)}{S(X)}$.

Діаграми дерева

Для розв'язання складних багатоступеневих задач використовують деревоподібні діаграми. Вони допомагають структурувати всі можливі сценарії.

• Ймовірності множаться горизонтально вздовж гілок (подія $A$ І $B$).

• Ймовірності додаються вертикально між різними гілками (подія $A$ АБО $B$).

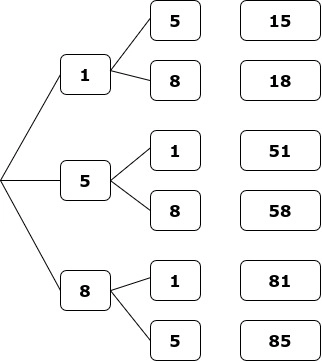
Приклад

Скільки різних двозначних чисел можна скласти з цифр 1, 5 і 8, якщо кожну цифру використовувати у числі тільки один раз?