Трикутники

Означення

Трикутник — це найпростіший многокутник, що має три вершини та три сторони. Він є базовим елементом планіметрії, оскільки будь-яку іншу фігуру можна розбити на трикутники.

Класифікація трикутників

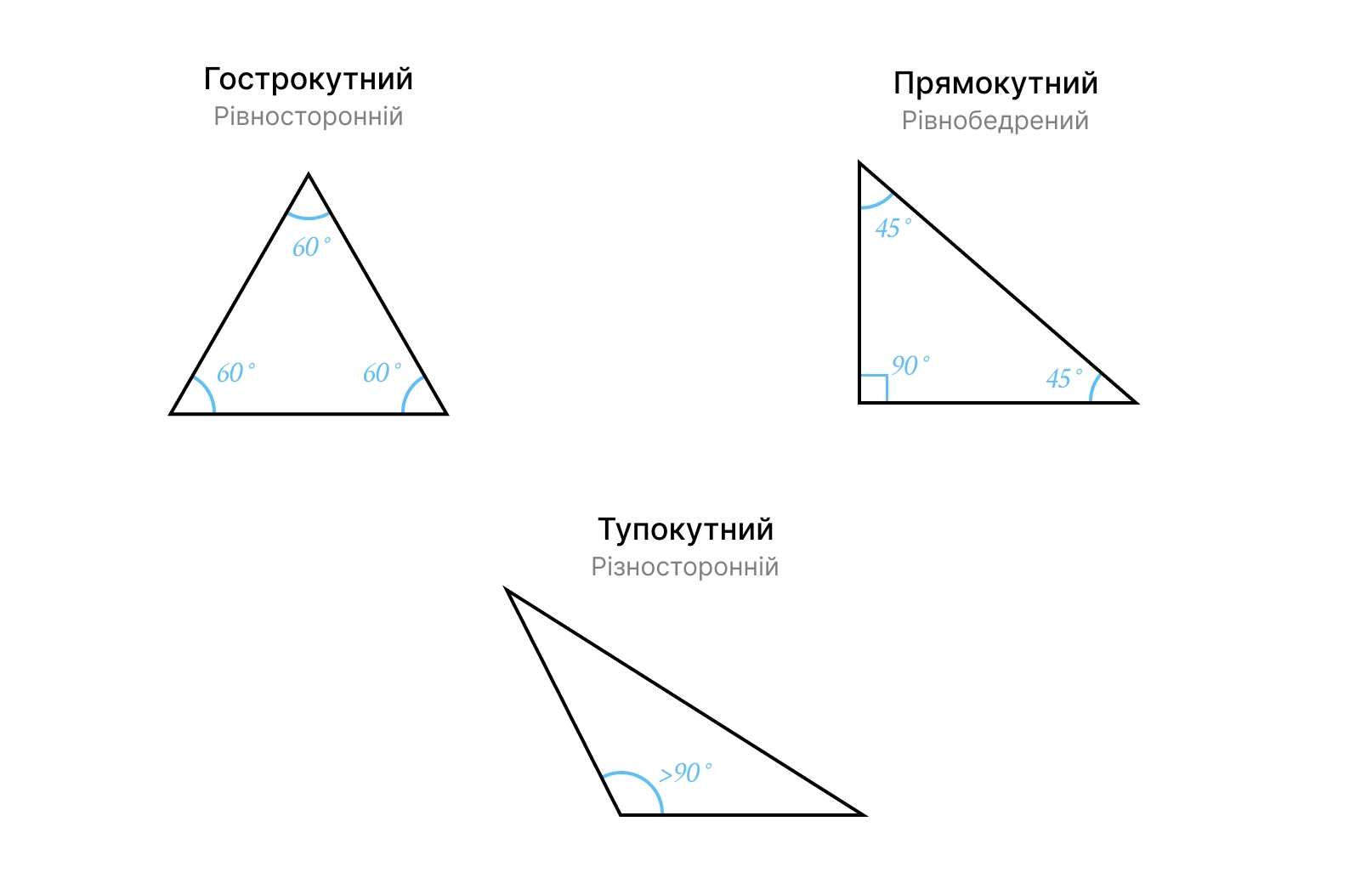
Трикутники класифікують за двома основними ознаками:

Важливі лінії та властивості

• Сума кутів: Завжди становить $180^{\circ }$.

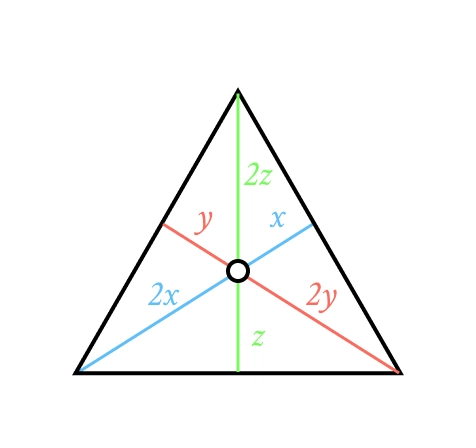
• Медіана: Сполучає вершину з серединою протилежної сторони. Усі три медіани перетинаються в одній точці (центроїді), яка ділить кожну медіану у відношенні 2:1, починаючи від вершини.

• Бісектриса: Ділить кут навпіл. Точка перетину бісектрис — центр вписаного кола.

• Висота: Перпендикуляр до протилежної сторони. Точка перетину висот називається ортоцентром.

• Середня лінія: Сполучає середини двох сторін. Вона паралельна третій стороні та дорівнює її половині.

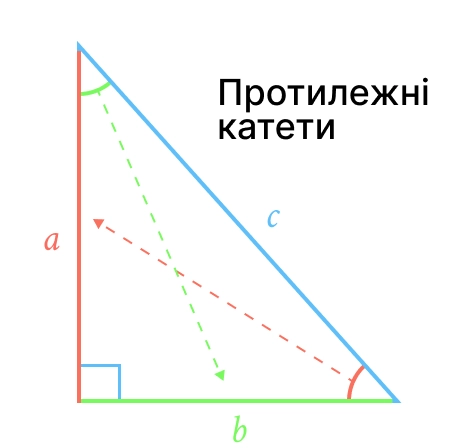
Прямокутний трикутник

Має унікальні властивості, що найчастіше використовуються в задачах:

• Теорема Піфагора: $a^2+b^2=c^2$.

• Тригонометричні співвідношення: $\sin \alpha =\frac{a}{c}$, $\cos \alpha =\frac{b}{c}$.

• Медіана до гіпотенузи: Дорівнює її половині та є радіусом описаного кола.

Формули площі

Вибір формули залежить від відомих елементів:

1. Класична: $S=\frac{1}{2}a{h}_a$

2. За двома сторонами та кутом: $S=\frac{1}{2}ab\sin \gamma$

3. Формула Герона: $S=\sqrt{p(p-a)(p-b)(p-c)}$, де $p$ — півпериметр ($\frac{a+b+c}{2}$).