Координати та вектори у просторі

У стереометрії для опису положення об'єктів використовується тривимірна система координат. До осей Ox (абсцис) та Oy (ординат) додається третя вісь — Oz (вісь аплікат), що перпендикулярна до площини $x y$ .

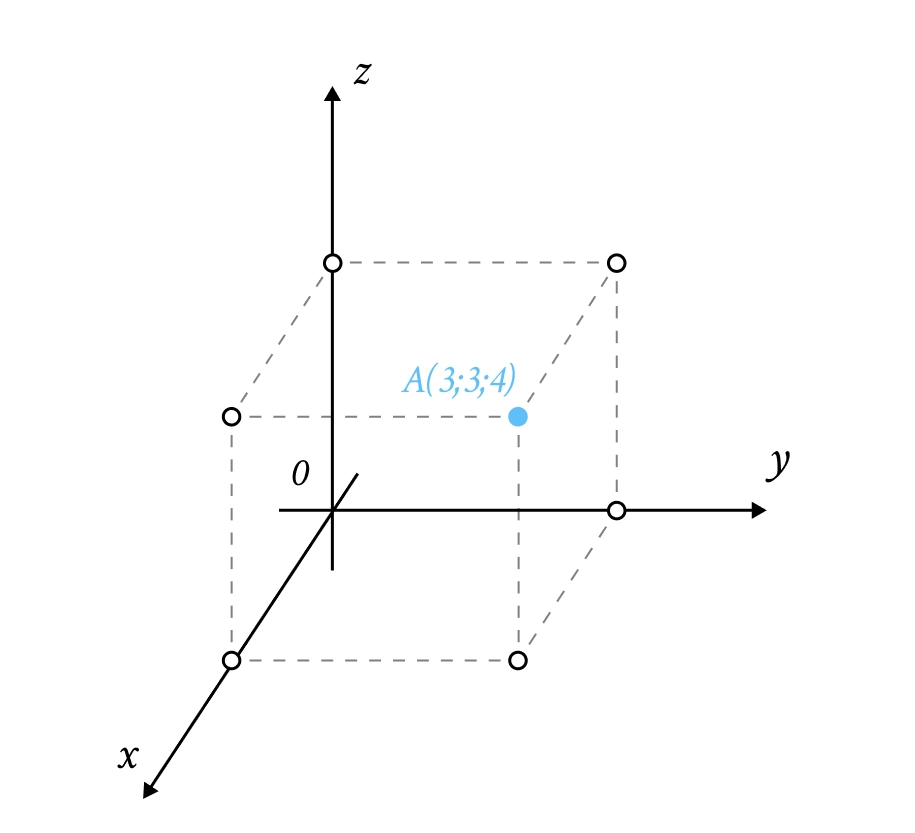
Декартові координати у просторі

Будь-яка точка $M$ задається трійкою чисел $(x; y; z)$ . Важливо розуміти логіку розміщення:

Якщо точка лежить на осі, то дві її інші координати дорівнюють $0$ (наприклад, на $O z$ : $(0; 0; z)$ ).
Якщо точка лежить у координатній площині, то одна координата дорівнює $0$ (наприклад, у $x z$ : $(x; 0; z)$ ).

Основні метричні формули

Відстань між точками $A$ і $B$ :
$d = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} + (z_{2} - z_{1})^{2}$
Координати середини відрізка: Обчислюються як середнє арифметичне відповідних координат кінців $A$ та $B$ .

Вектори у просторі

Вектори у просторі працюють за тими ж принципами, що й на площині, але з додаванням компоненти $z$ .

Координати вектора: $A B = (x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})$ .
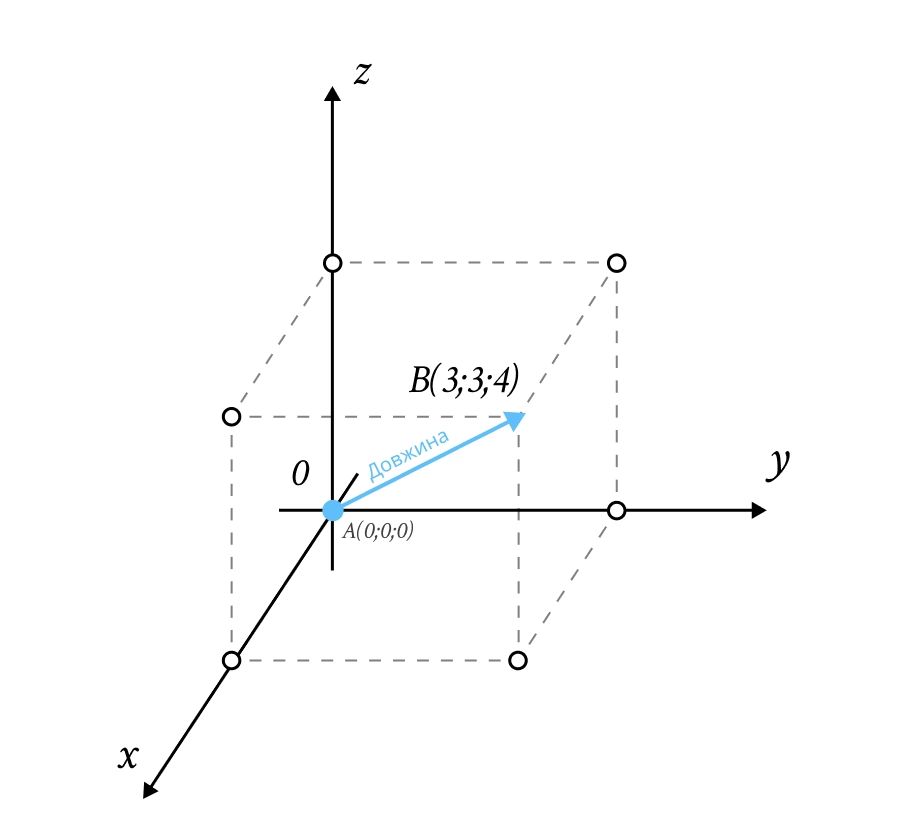
Довжина (модуль) вектора: $∣ a ∣ = a_{x}^{2} + a_{y}^{2} + a_{z}^{2}$ .

Операції та умови

Операція/Умова	Математичний вираз
Скалярний добуток	$a \cdot b = a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z}$
Перпендикулярність	$a \cdot b = 0$
Колінеарність (паралельність)	$\frac{a _{x}}{b _{x}} = \frac{a _{y}}{b _{y}} = \frac{a _{z}}{b _{z}}$

Додавання та множення: Вектори додаються покомпонентно. При множенні вектора на число $k$ кожна його координата множиться на цей коефіцієнт.