Планіметрія — це розділ геометрії, що вивчає фігури на площині. Всі побудови базуються на неозначуваних поняттях (точка, пряма) та аксіомах — твердженнях, що приймаються без доведення.
Найпростіші фігури та аксіоми
Точка: найпростіша одиниця простору (позначається ).
Пряма: нескінченна лінія, що не має товщини (позначається або ).
Фундаментальні аксіоми:
Через будь-які дві точки можна провести пряму, і до того ж тільки одну.
Яка б не була пряма, існують точки, що належать їй (), і точки, що не належать їй ().
Із трьох точок на прямій одна і тільки одна лежить між двома іншими.
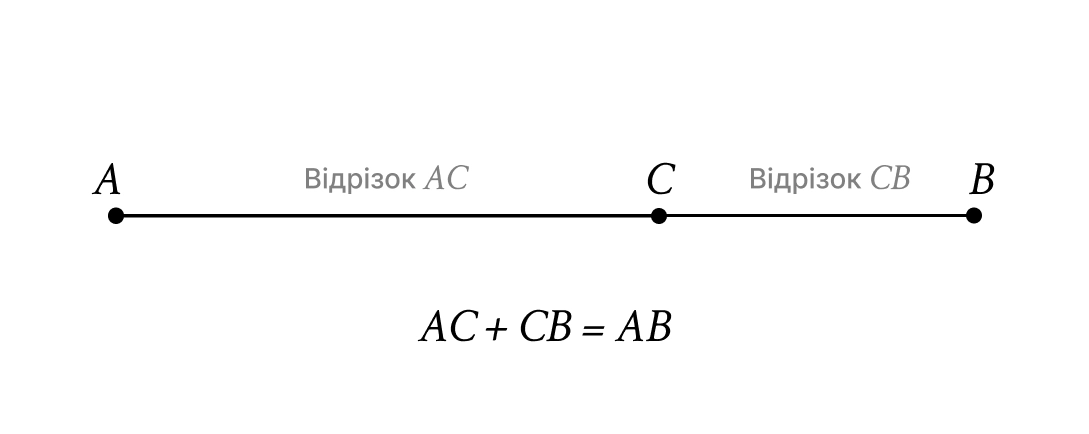
Відрізок та промінь
Відрізок — частина прямої, обмежена двома точками. Його довжина завжди є додатним числом. Якщо точка лежить між та , то .
Промінь (півпряма) — частина прямої, що має початок, але не має кінця. Два промені зі спільним початком, що утворюють пряму, називаються доповняльними.
Кути та їхні види
Кут — це фігура, утворена двома променями (сторонами), що виходять з однієї точки (вершини). Промінь, що ділить кут навпіл, називається бісектрисою.
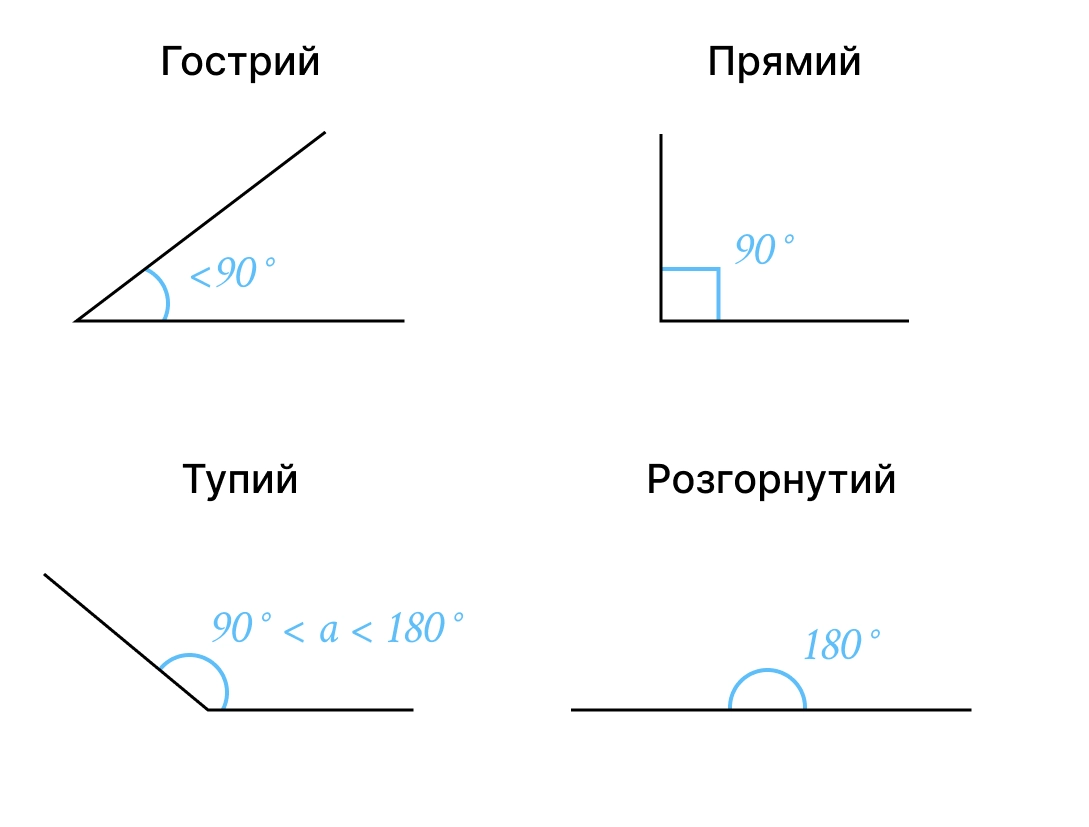
Вид кута | Градусна міра |
Гострий | Менше |
Прямий | Рівно |
Тупий | Від до |
Розгорнутий | Рівно |
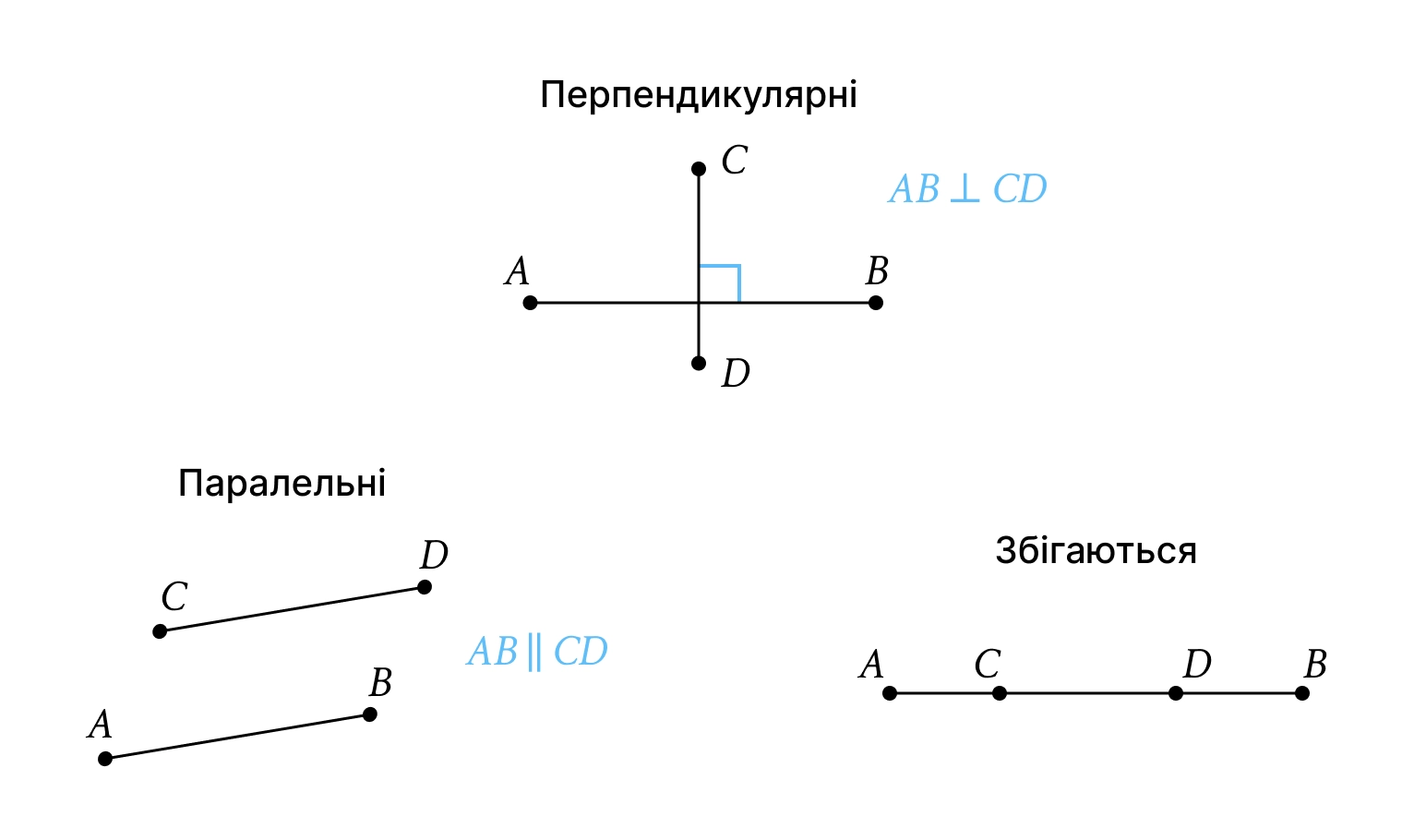
Взаємне розміщення прямих
Прямі на площині можуть:
Перетинатися: мають одну спільну точку. Якщо кут перетину , прямі називаються перпендикулярними ().
Бути паралельними: ніколи не мають спільних точок ().
Збігатися: мають дві або більше спільних точок.
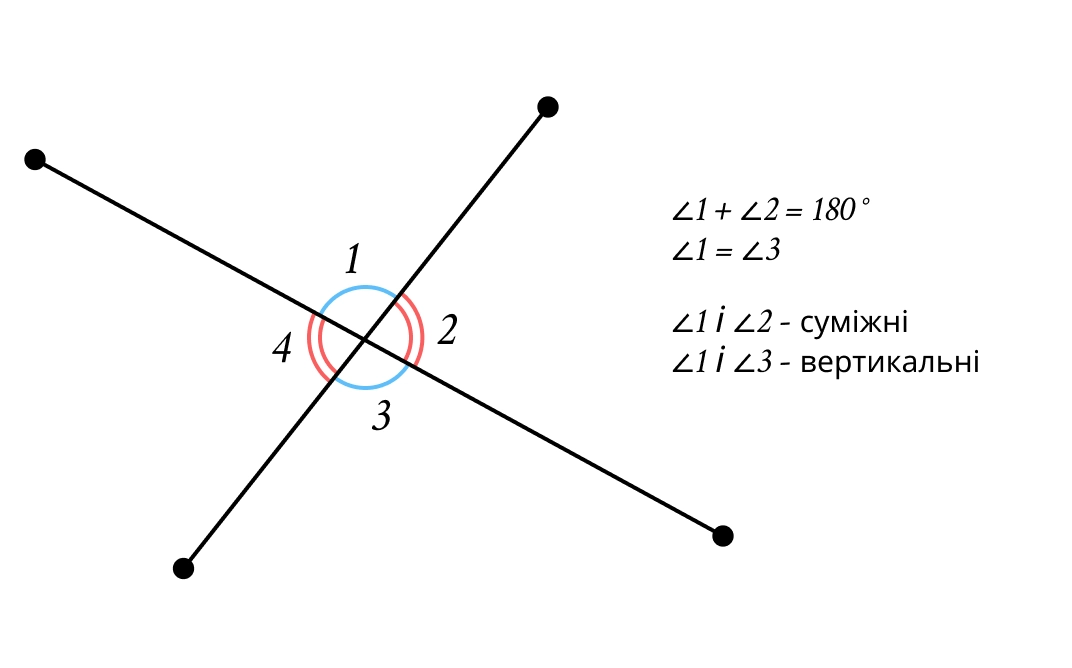
Кути при перетині прямих:
Суміжні кути: мають спільну сторону, а їхня сума завжди дорівнює .
Вертикальні кути: утворюються при перетині двох прямих і лежать навпроти один одного. Вони завжди рівні.