Елементарні функції є «цеглинками», з яких будуються складніші математичні моделі. Кожна з них має свій характерний вигляд графіка та специфічні властивості.
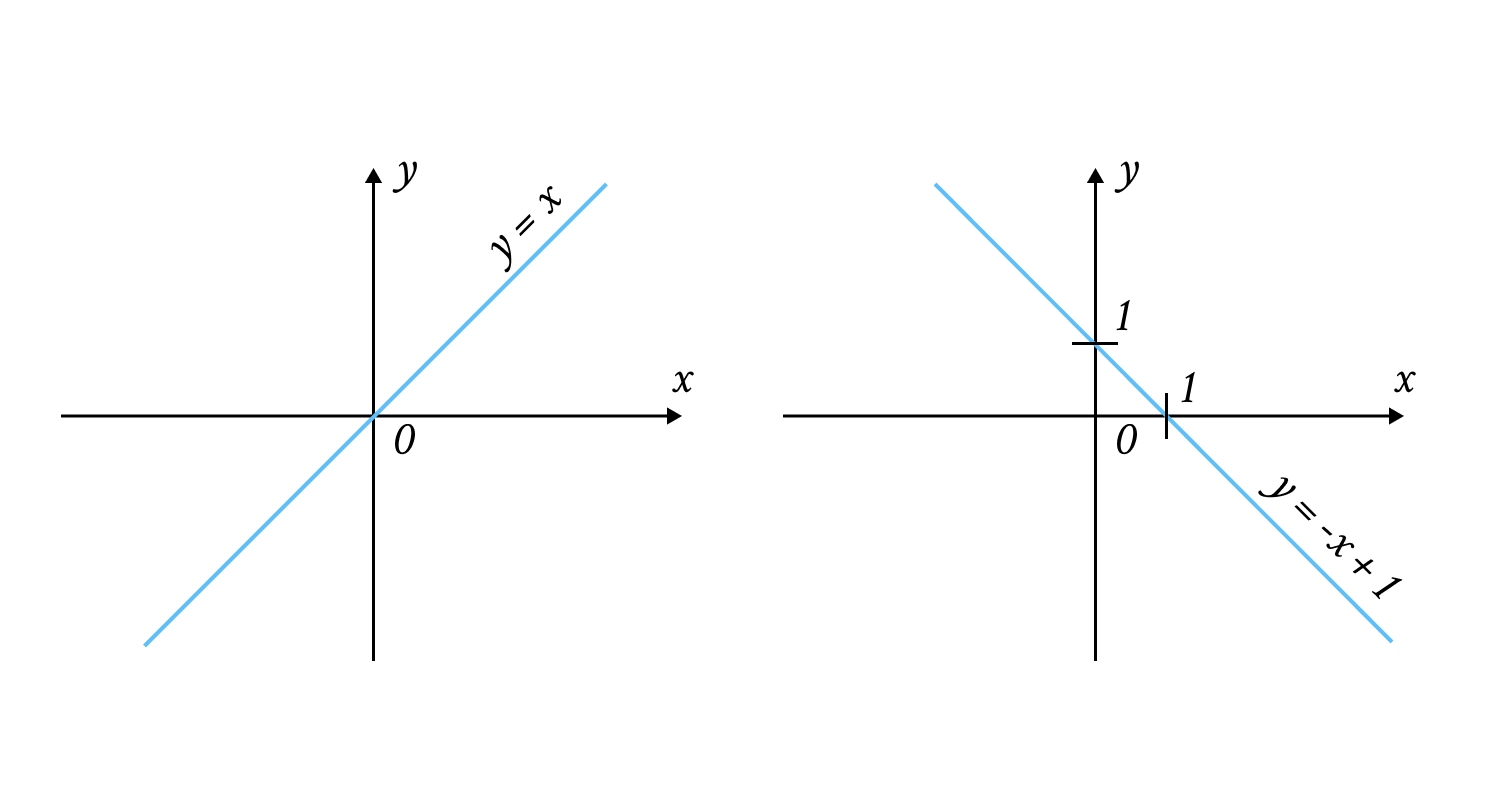
Лінійна та квадратична функції
Лінійна функція (): Графіком є пряма лінія. Коефіцієнт (кутовий коефіцієнт) відповідає за нахил: при функція зростає, при — спадає.
Квадратична функція (): Графіком є парабола. Координата вершини обчислюється як .
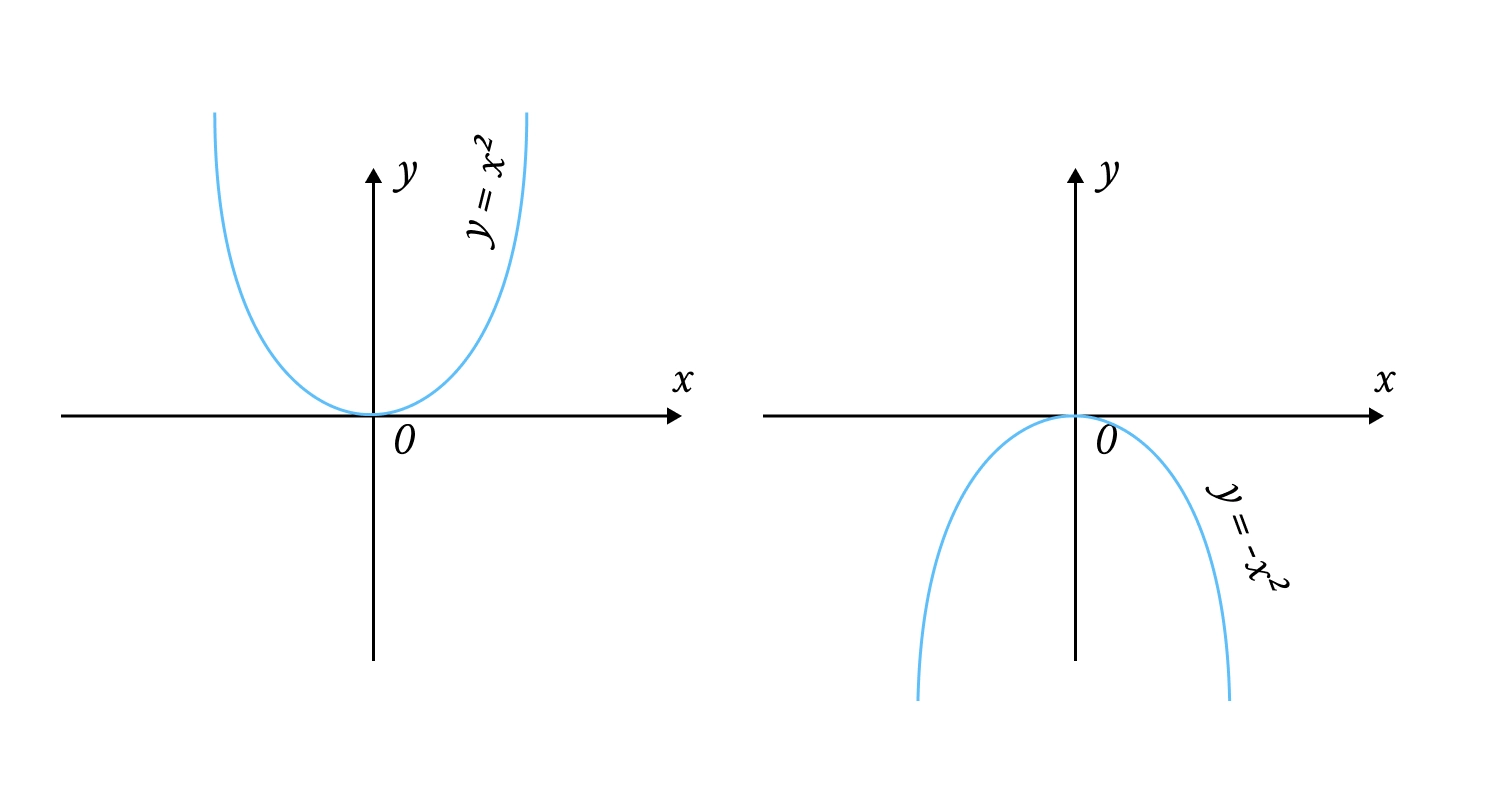
Обернена пропорційність, степенева та коренева функції
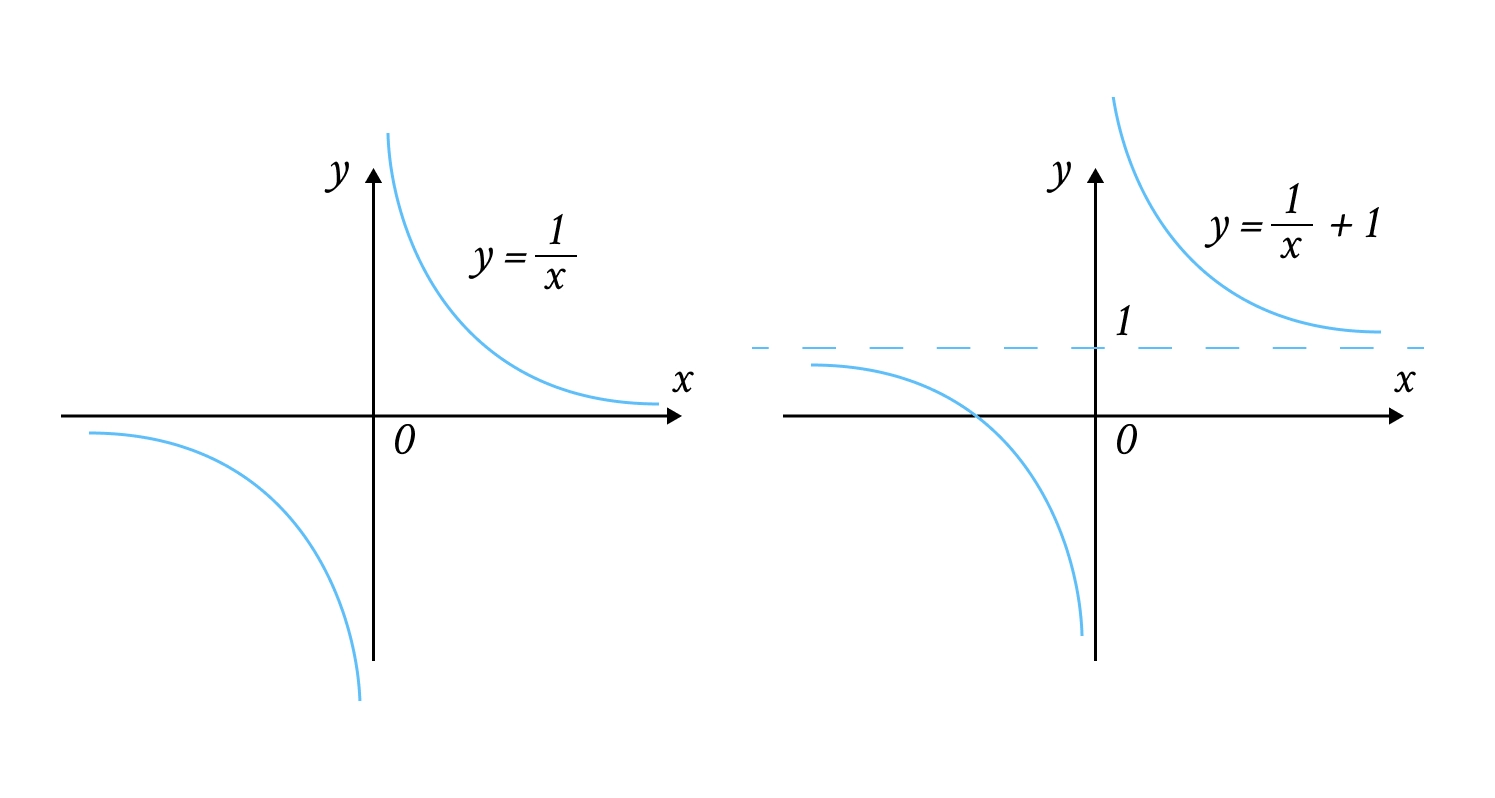
Обернена пропорційність (): Графік — гіпербола. Осі координат виступають асимптотами — лініями, до яких графік наближається, але ніколи їх не торкається.
Степенева функція (): При парному (наприклад, , а взагалі парне число зазвичай записують як , а непарне як ) графік симетричний відносно осі ; при непарному — це кубічна парабола, симетрична відносно початку координат.
Коренева функція (): При парному (наприклад, ) функція визначена тільки для , а графік — вітка параболи, що лежить «на боці»; при непарному , функція визначена для всіх , а графік — симетричний відносно початку координат.
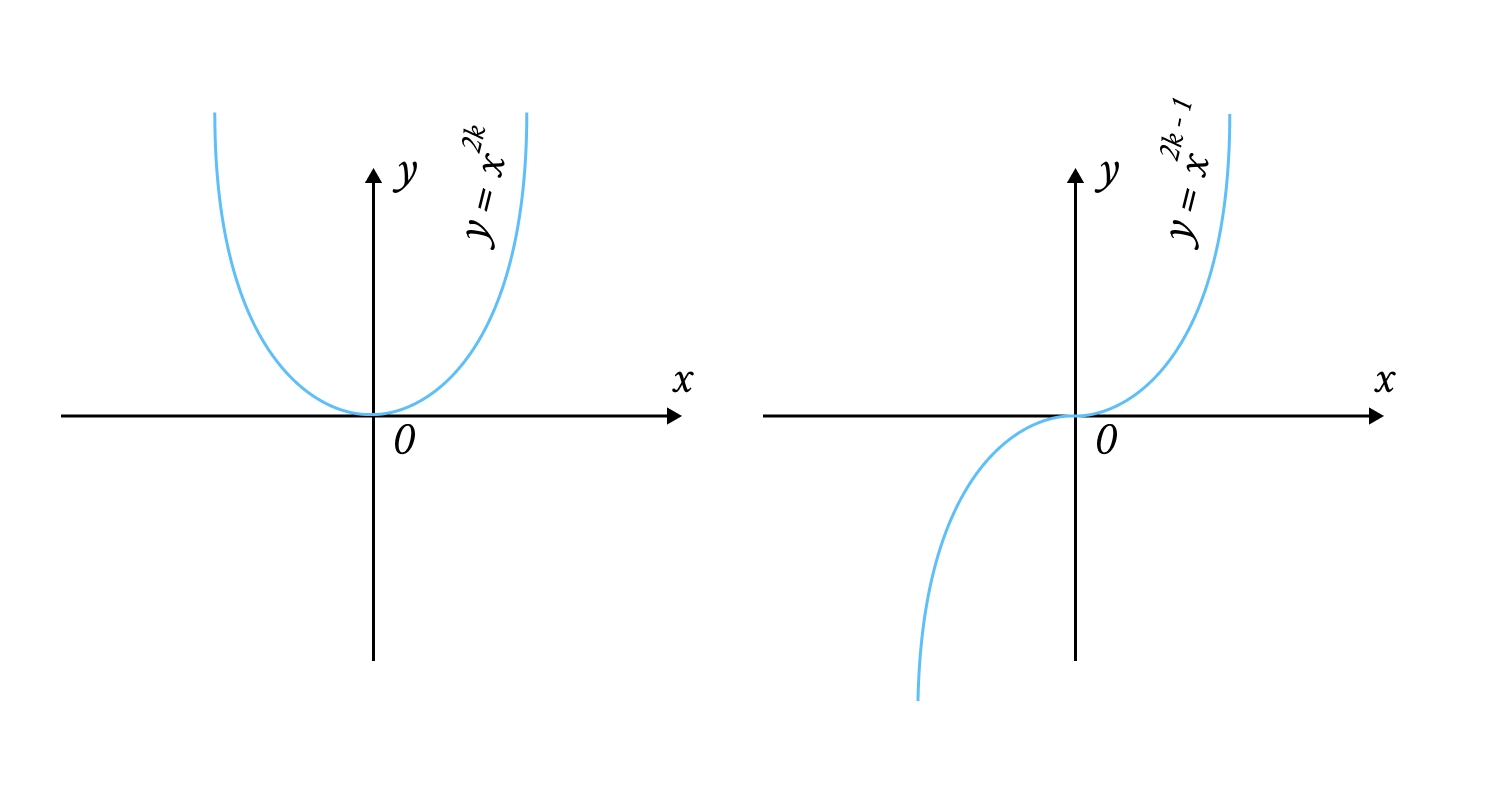
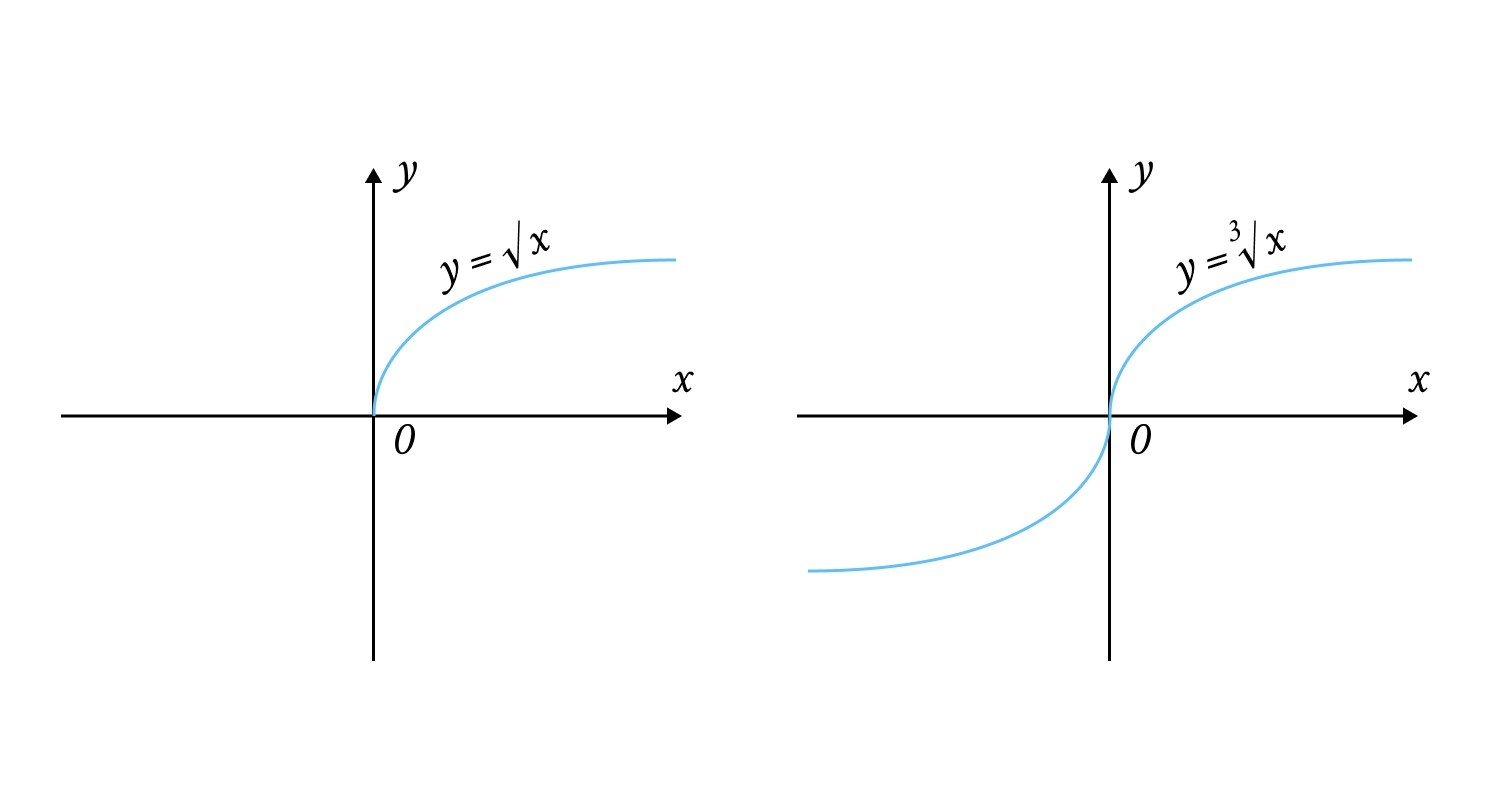
Показникова та логарифмічна функції
Ці функції є взаємно оберненими, а їхні графіки симетричні відносно прямої .
Показникова (): Завжди проходить через точку . При стрімко зростає.
Логарифмічна (): Визначена тільки для . Завжди проходить через точку .
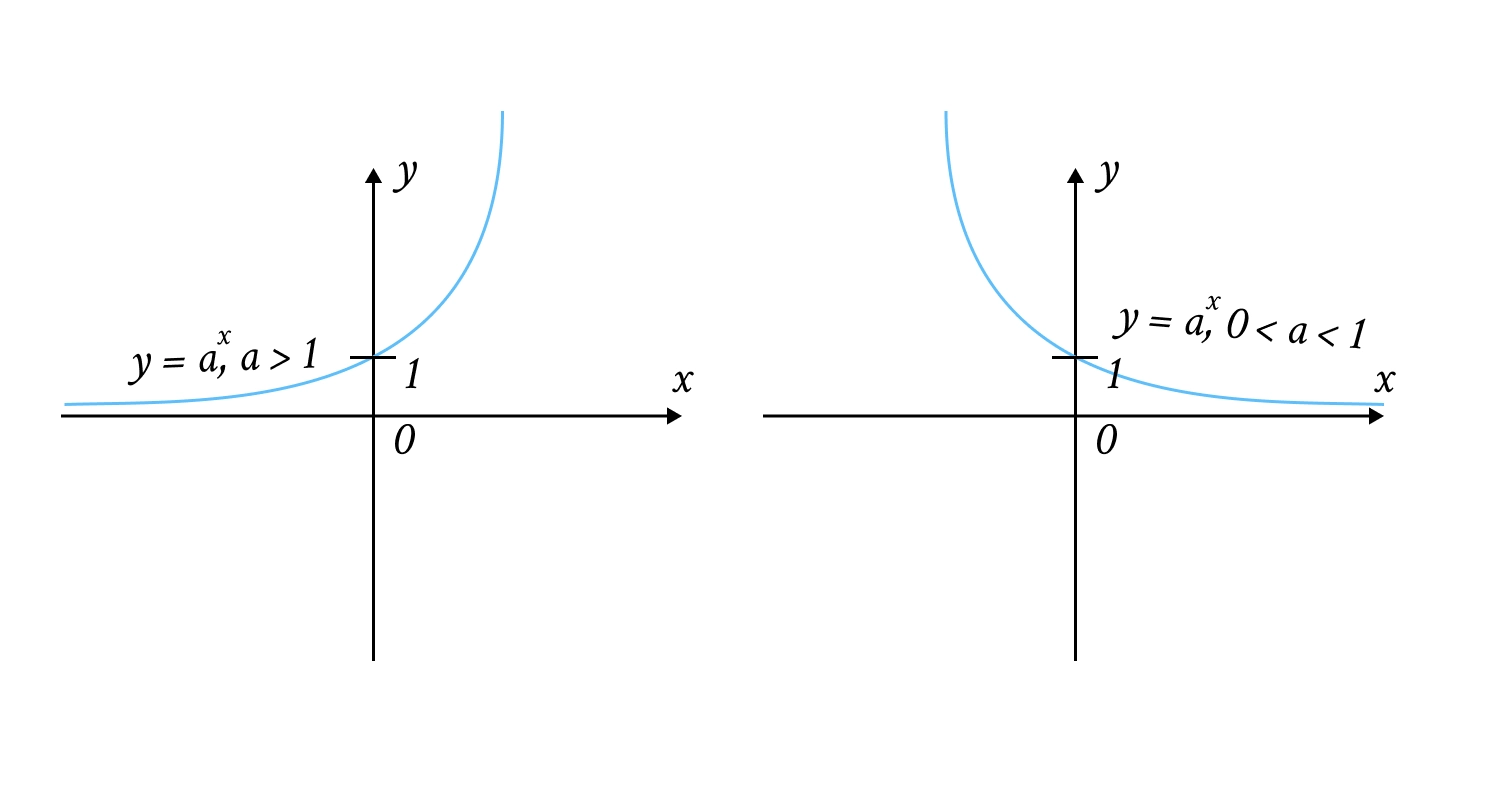
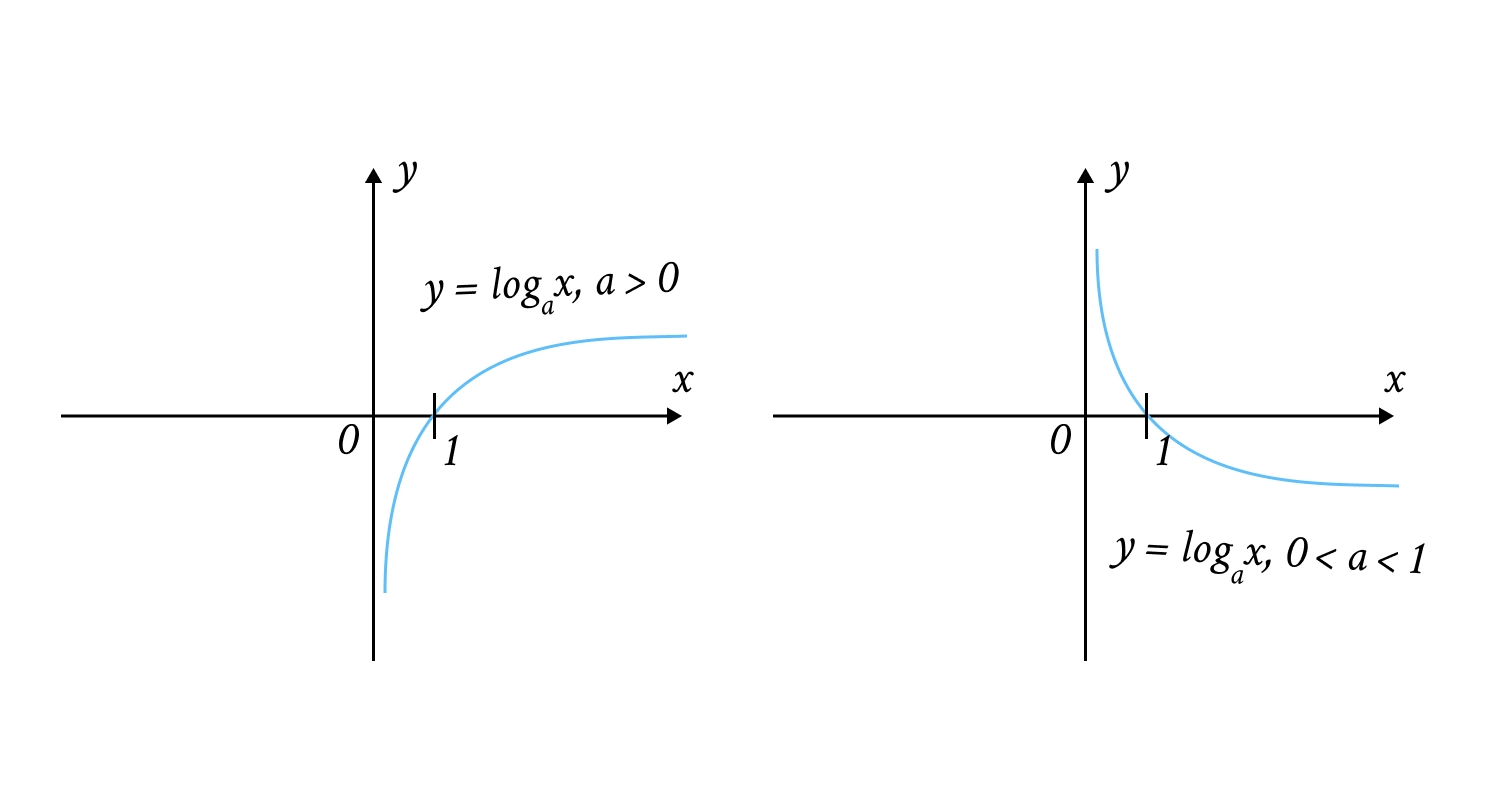
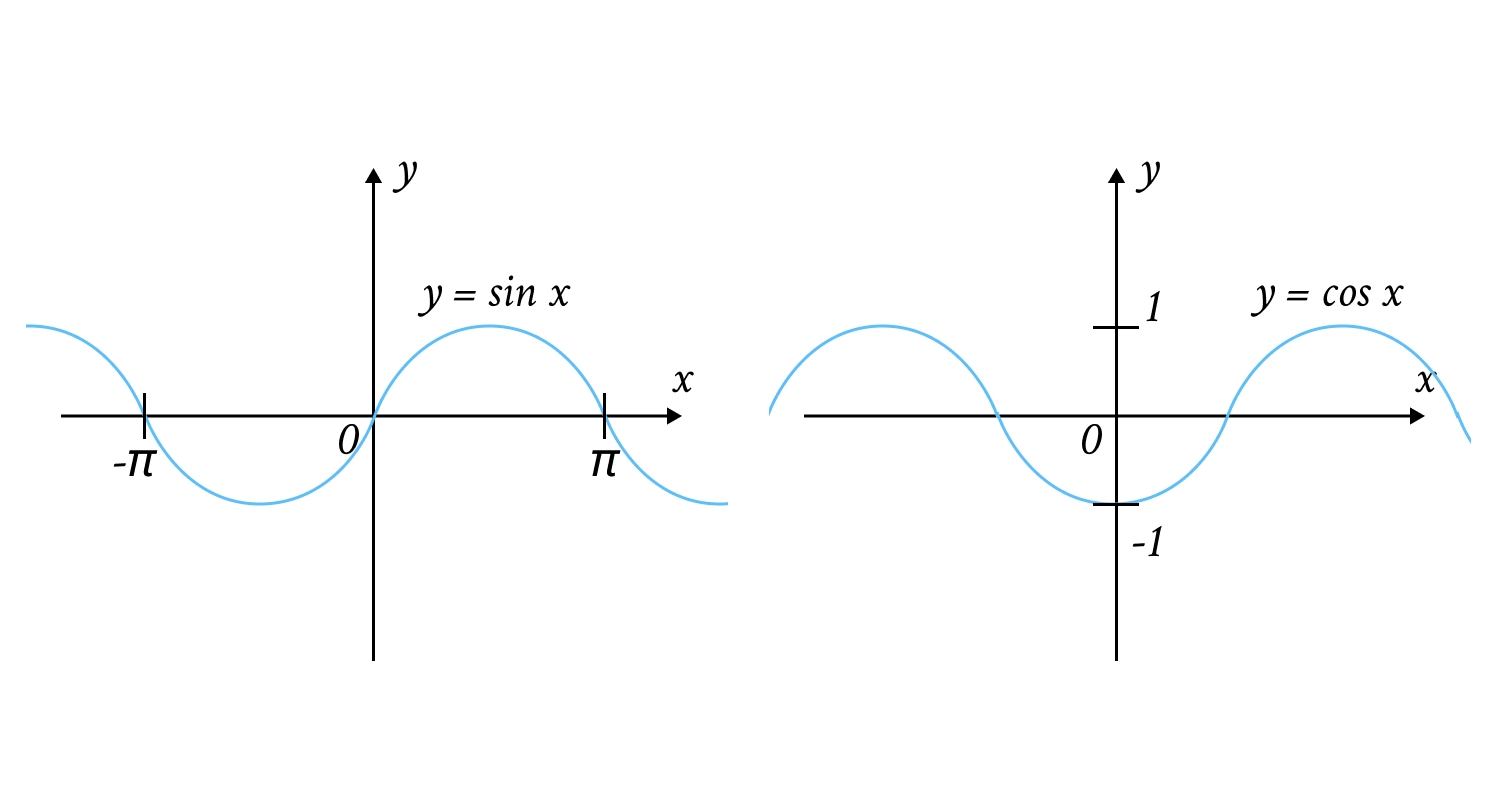
Тригонометричні функції
Описують періодичні процеси (коливання):
Функція | Графік | Властивість |
Синусоїда | Проходить через , непарна. | |
Косинусоїда | Проходить через , парна. | |
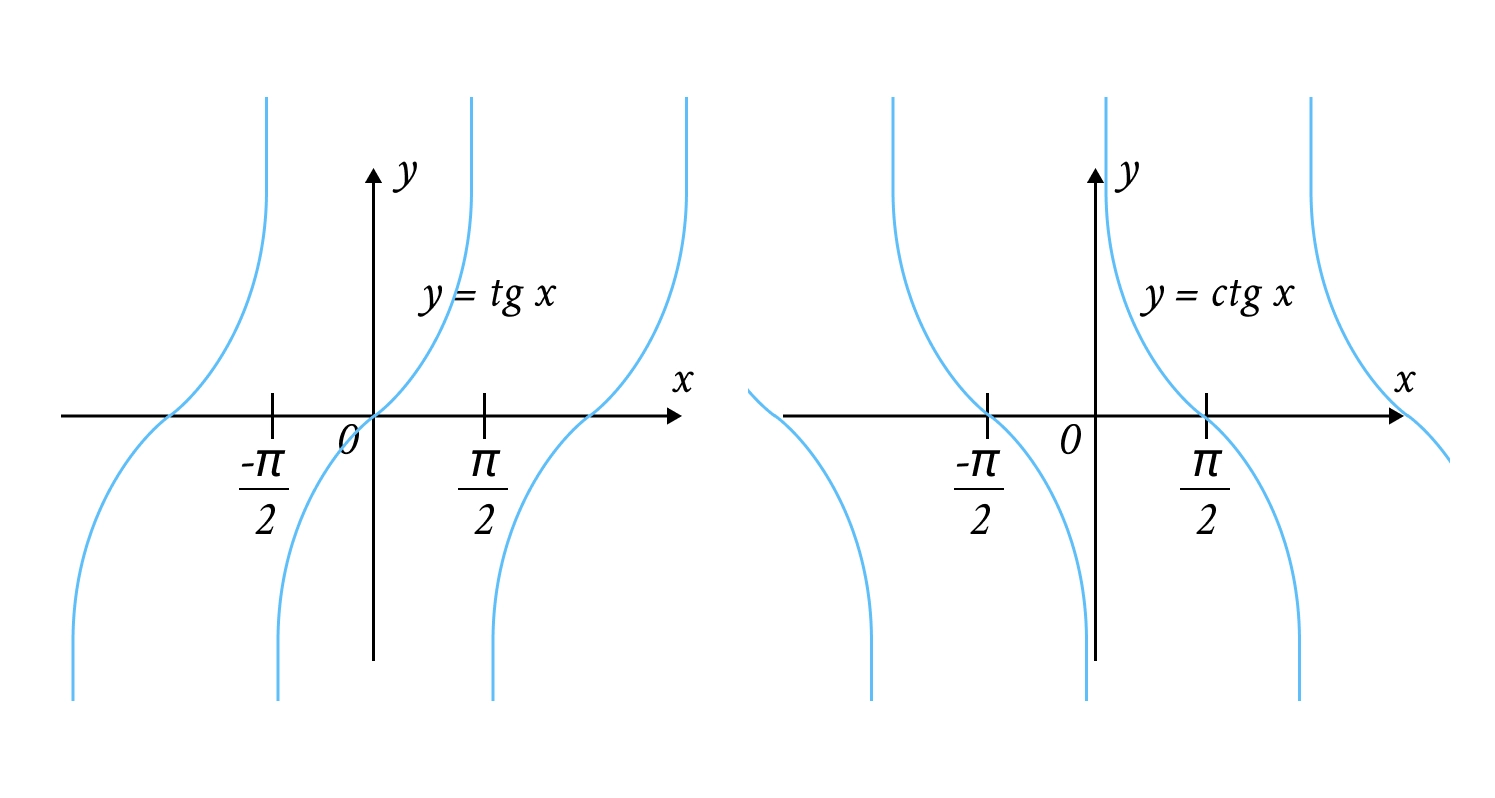
Тангенсоїда | Має розриви в точках . | |
Котангенсоїда | Має розриви в точках . |